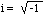 . The a represents the
real part of the complex constant and b represents the imaginary part.
This complex constant is stored in the computer as the ordered
pair (a, b).
. The a represents the
real part of the complex constant and b represents the imaginary part.
This complex constant is stored in the computer as the ordered
pair (a, b).
Computers are great data manipulators and mathematicians. However, they must be given data and numbers on which to act. Solving problems with a computer involves inputting some data, having the program manipulate the data in some way, and outputting the data in a different and more useful form.
Example: Carbon Dating Carbon dating is a method for estimating the age of organic substances. It compares the amount of carbon 14 contained in the remains of the substance with the amount of carbon 14 that would have been in the object's environment at the time it was alive. A mathematical formula is used to determine the age of the object based on the carbon 14 proportion remaining in the substance. If a computer is used to solve this equation, there must be some means of communicating the carbon 14 proportion remaining in the object to the computer. Numerical and character values are established in a computer program by the use of constants and variables. Constants are values used directly in the program. Variables represent memory locations that are given a name.
Integer constants are constants that do not contain a decimal point.
The size of integer that can be stored in a computer depends on the computer itself. If the integer is stored in 4 bytes or 32 bits (1 byte=8 bits), the largest positive number that can be represented is (2**31-1) or 2147483647 and the smallest negative number that can be represented is -(2**31) or -2147483548.
Real constants contain a decimal point and may or may not have digits past the decimal point. A REAL constant - 0.0001216 - will be used in the formula for carbon 14 dating problem.
Real constants are also called floating-point constants and can be expressed in exponential notation. Exponential notation expresses a value as a number between 0.1 and 1 multiplied by an appropriate power of 10. The E represents "exponent of 10".
Due to the way that real numbers are stored, their size limit depends on the computer but is typically between -10E38 and +10E38, much larger than it was for integers.
Double Precision constants are reals which are stored with more digits of accuracy than single precision constants, sometimes with more than twice as many digits. The exact number of digits stored depends on the computer. Single precision and double precision constants have the same range, but double-precision values store those numbers with more digits of precision. A double precision constant is written in an exponential form with a D instead of an E.
Complex constants are often used in physics and engineering.
They have the form a+bi, where a and b are real numbers and
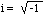 . The a represents the
real part of the complex constant and b represents the imaginary part.
This complex constant is stored in the computer as the ordered
pair (a, b).
. The a represents the
real part of the complex constant and b represents the imaginary part.
This complex constant is stored in the computer as the ordered
pair (a, b).
Character constants consist of a string of arbitrary length of characters enclosed in apostrophes. The apostrophes are not counted when determining the length of the character string.
Examples
Blanks are significant characters in character strings; therefore, the value of 'a string' is not the same as the value of 'astring'. Note that in the last example two consecutive single apostrophes are used to represent the single apostrophe.
Logical constants have one of two values, either .TRUE. or .FALSE.
Using a box to represent a memory cell, a label to represent the name or address of the memory cell (bottom left corner) and the type of contents stored in the box (bottom right corner), the following shows a model of the variable myage whose content is 23.

A variable name
In the FORTRAN language, there is no difference between upper and lower case letters.
All variables in this textbook will be explicitly typed.
In the carbon 14 dating example, a
variable of type
REAL would be declared to reference a memory location where the value
representing the proportion of carbon 14 remaining in the
artifact is located.
REAL :: carbon
2. What are the rules for naming variables? Use these rules to find the three unacceptable names in the following list and explain why each is invalid.
3. Express each of the following in exponential form with the given exponent:
4. Names chosen for variables should be descriptive and explicitly typed. For example, COUNT would be a descriptive name for a variable that keeps a count of items. TOTAL_COST is a good name for a sum of expenditures.
As a train travels over a straight section of track, it exerts a both downward force, equivalent to the weight of the train, and a horizontal force, called centrifugal force. Centrifugal force is a function of the weight of the train, its speed as it rounds the curve, and the radius of the curve. Assign a descriptive variable name to each of the following:
5. Write declaration statements for variables which describe the following. Take into consideration whether the items are likely to be real, integer or character.