Infinite families of links with trivial Jones polynomial, by Shalom Eliahou, Louis H. Kauffman and Morwen Thistlethwaite (pdf, 330 Kb)
Added March 22, 2001:
We have found a common
explanation for the sequences presented below, and are now able to prove:
Theorem. Let L be any link with k >= 1
components; let VL be the Jones polynomial of L, and let u denote the
Jones polynomial of the unlink of two components, i.e. u = -t-1/2 - t1/2.
Then there are infinitely many distinct prime links with (k+1) components whose Jones
polynomial is equal to uVL.
Corollary. For each k >= 2 there are infinitely many prime k-component
links with Jones polynomial equal to that of the k-component unlink.
Full details will appear shortly. Here are three examples:
A prime 4-component link
with Jones polynomial u3
A prime 5-component link
with Jones polynomial u4
A prime 6-component link
with Jones polynomial u5
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
These links are all satellites of the Hopf link.
The accompanying pictures were produced with the help of
Kenneth Stephenson's
circle packing program.
(i) The family of 2-component links LL1(n) (n any integer).
For even n, the Jones polynomial of LL1(n) is precisely the Jones polynomial of
the 2-component unlink, whereas for odd n the polynomial is equal to the unlink polynomial
times t6 or t-6, depending on choices of orientation.
LL1(n) is formed by clasping together the numerator of the
rational tangle n · 1 · 1 · 1 · 2 with the numerator
of the rational tangle -3 , as illustrated below.
For positive n the resulting diagram has n + 16 crossings, and
for n <= 0 we get a diagram with |n| + 16 crossings reducible to
|n| + 15 crossings, except that for n = -1 we can reduce to 14 crossings.
Indeed, an exhaustive search has shown that LL1(-1), LL1(0) are the only links of up to 15
crossings with Jones polynomial equal to the unlink polynomial times a power of t.
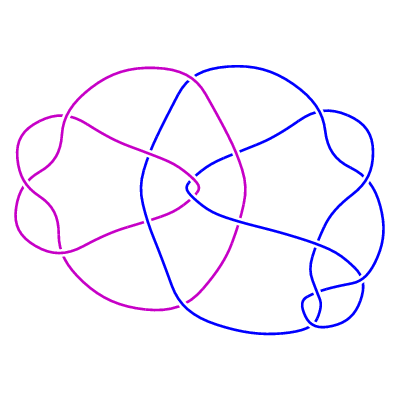
LL1(1)
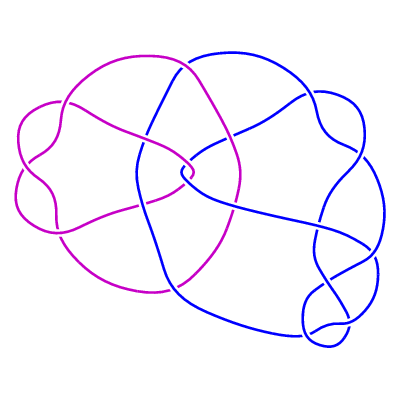
LL1(2)
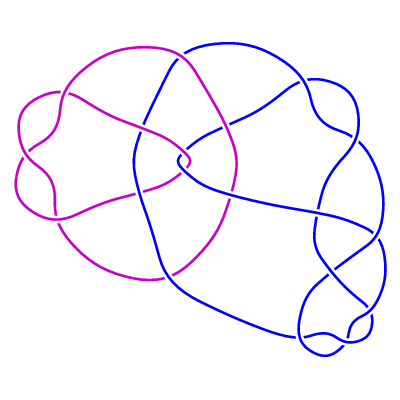
LL1(3)
(ii) The family of 2-component links LL2(n) (n>=0).
The Kauffman bracket polynomial of LL2(n) is equal to that of the 2-component unlink for all n.
However, the writhe is 0 for n even , and 8 (or -8) for n odd. Therefore, as with the
previous family, the Jones polynomial of LL2(n) is equal to that of the 2-component unlink
for all even n, but for odd n is equal to the unlink polynomial times a factor
t6 or t-6.
The link LL2(n) is formed similarly from the rational tangle
5 · 1 · 4 · 1 · 4 · 1 · ...
· 4 · 1 · 2
(where there are n occurrences of the pair 4 · 1 )
and its mirror-image, giving a diagram of 10n+24 crossings.
Here are pictures of LL2(0) and LL2(1):
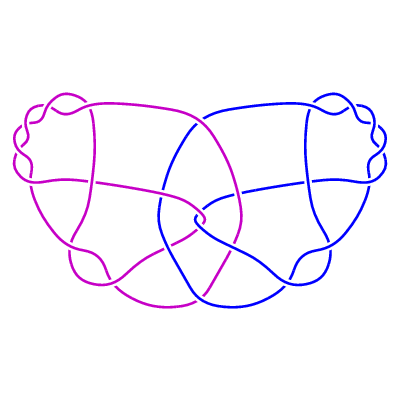
LL2(0)
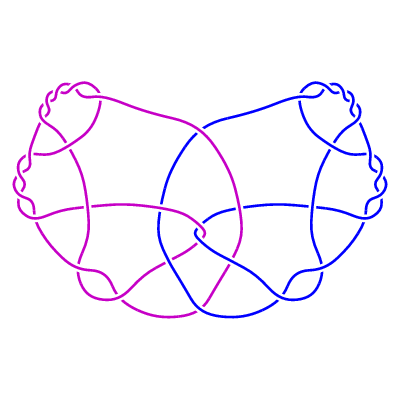
LL2(1)
(iii) The family of 3-component links LLL(n) (n>=0).
The Jones polynomial of LLL(0) is equal to that of the 3-component unlink if one chooses
orientations of the blue and green strands so that the writhe of the diagram is 2,
whereas for n >= 1 the Jones polynomial of LLL(n) is equal to that of the 3-component
unlink unconditionally.
This time we use the rational tangle -3 together with the "generalized rational
tangle"
2 · 1/2 · 1 · 1/2 · 1 ...
· 1/2 · 1 · 1 · 2
( n occurrences of the pair 1/2 · 1 )
producing a diagram with 3n+16 crossings.
Here are the first four links in this sequence:
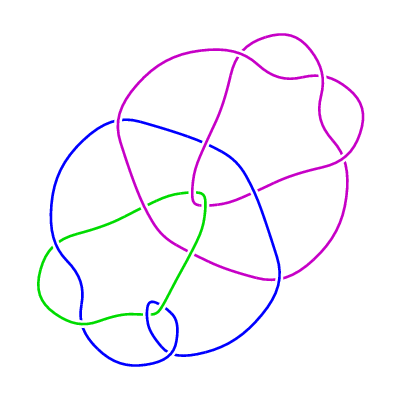
LLL(0)
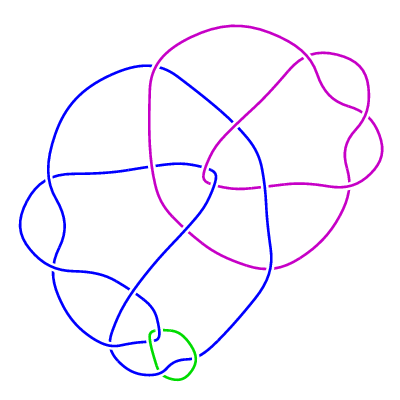
LLL(1)
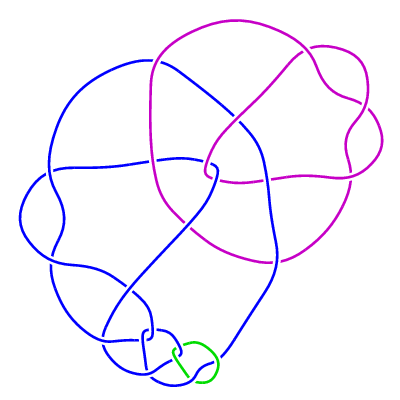
LLL(2)
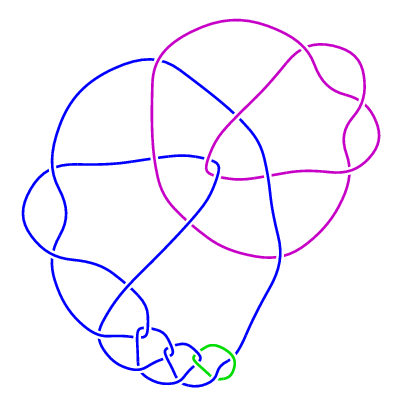
LLL(3)
Added March 5, 2001: The family of 2-component links LL1(m, n)
(m>=0 , n any integer).
Further investigation has shown that the original family
LL1(n) is the 1-parameter subfamily corresponding to m = 0 of this new 2-parameter family.
LL1(m, n) is constructed from the rational tangle -3 , together with
n · 1 · 1 · 1/2 · 1 · 1/2 · 1 ...
· 1/2 · 1 · 1 · 2
(m occurrences of the pair 1/2 · 1 ).
For m >= 1 the Jones polynomial of LL1(m, n) is precisely equal to that of the unlink of
two components. Here are some examples:
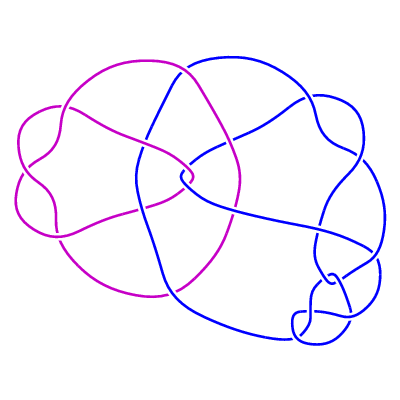
LL1(1, 1)
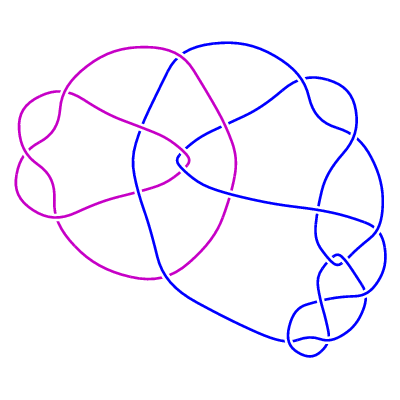
LL1(1, 2)
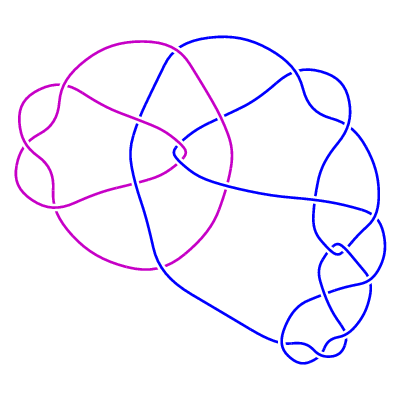
LL1(1, 3)
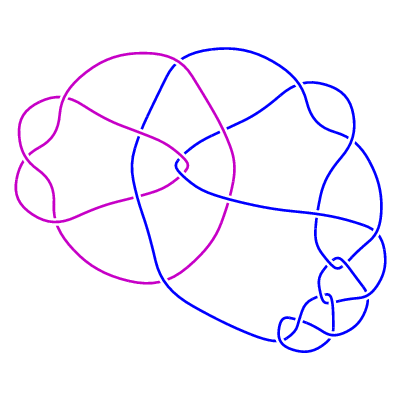
LL1(2, 1)
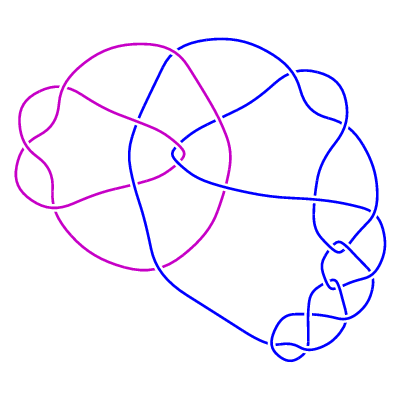
LL1(2, 2)
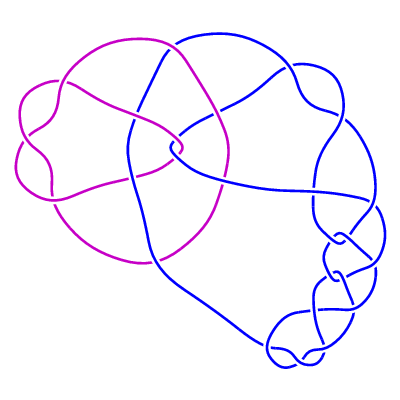
LL1(2, 3)
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
The accompanying pictures were produced with the help of Kenneth Stephenson's circle packing program.
(i) The family of 2-component links LL1(n) (n any integer).
For even n, the Jones polynomial of LL1(n) is precisely the Jones polynomial of the 2-component unlink, whereas for odd n the polynomial is equal to the unlink polynomial times t6 or t-6, depending on choices of orientation.LL1(n) is formed by clasping together the numerator of the rational tangle n · 1 · 1 · 1 · 2 with the numerator of the rational tangle -3 , as illustrated below.
For positive n the resulting diagram has n + 16 crossings, and for n <= 0 we get a diagram with |n| + 16 crossings reducible to |n| + 15 crossings, except that for n = -1 we can reduce to 14 crossings. Indeed, an exhaustive search has shown that LL1(-1), LL1(0) are the only links of up to 15 crossings with Jones polynomial equal to the unlink polynomial times a power of t.

LL1(1)

LL1(2)

LL1(3)
(ii) The family of 2-component links LL2(n) (n>=0).
The Kauffman bracket polynomial of LL2(n) is equal to that of the 2-component unlink for all n. However, the writhe is 0 for n even , and 8 (or -8) for n odd. Therefore, as with the previous family, the Jones polynomial of LL2(n) is equal to that of the 2-component unlink for all even n, but for odd n is equal to the unlink polynomial times a factor t6 or t-6.The link LL2(n) is formed similarly from the rational tangle 5 · 1 · 4 · 1 · 4 · 1 · ... · 4 · 1 · 2 (where there are n occurrences of the pair 4 · 1 ) and its mirror-image, giving a diagram of 10n+24 crossings. Here are pictures of LL2(0) and LL2(1):

LL2(0)

LL2(1)
(iii) The family of 3-component links LLL(n) (n>=0).
The Jones polynomial of LLL(0) is equal to that of the 3-component unlink if one chooses orientations of the blue and green strands so that the writhe of the diagram is 2, whereas for n >= 1 the Jones polynomial of LLL(n) is equal to that of the 3-component unlink unconditionally.This time we use the rational tangle -3 together with the "generalized rational tangle"
2 · 1/2 · 1 · 1/2 · 1 ... · 1/2 · 1 · 1 · 2 ( n occurrences of the pair 1/2 · 1 ) producing a diagram with 3n+16 crossings. Here are the first four links in this sequence:

LLL(0)

LLL(1)

LLL(2)

LLL(3)
Added March 5, 2001: The family of 2-component links LL1(m, n) (m>=0 , n any integer).
Further investigation has shown that the original family LL1(n) is the 1-parameter subfamily corresponding to m = 0 of this new 2-parameter family. LL1(m, n) is constructed from the rational tangle -3 , together with
n · 1 · 1 · 1/2 · 1 · 1/2 · 1 ... · 1/2 · 1 · 1 · 2 (m occurrences of the pair 1/2 · 1 ).
For m >= 1 the Jones polynomial of LL1(m, n) is precisely equal to that of the unlink of two components. Here are some examples:

LL1(1, 1)

LL1(1, 2)

LL1(1, 3)

LL1(2, 1)

LL1(2, 2)

LL1(2, 3)

LL1(1, 1)

LL1(1, 2)

LL1(1, 3)

LL1(2, 1)

LL1(2, 2)

LL1(2, 3)