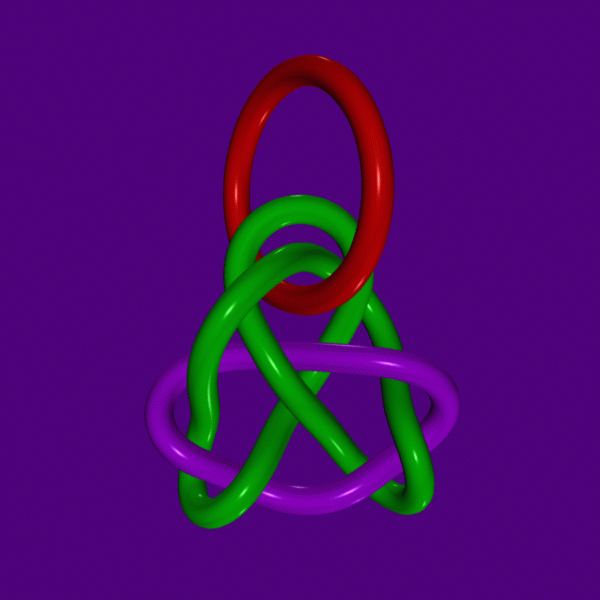Some symmetric links

The Borromean Rings

A picture of a 12-crossing alternating link, displaying
a symmetry of order 4. The complement of this link may be formed by glueing
together two ideal cube-octahedra.

These two cells then constitute the
canonical cell decomposition of the link.
The symmetry group of the link is Z2 x P, where P is the group of
rotational symmetries of a cube (equivalently of an octahedron.)

The same alternating link, displaying this time a symmetry of
order 3

A 12-crossing non-alternating link whose canonical cell decomposition
consists of a single ideal cube-octahedron.
The symmetry group of this link is the dihedral group D3.
However, the complement of the link
has extra symmetries that don't extend to the (S3, link) pair.
The symmetry group of the complement is isomorphic to the group P mentioned above,
and acts transitively on the four cusps.
Craig Hodgson has shown that the complement of this
link is double-covered by the complement of the alternating link shown above.
For alternating hyperbolic links it seems that the symmetry group of the
link complement is always equal to that of the (S3, link) pair,
but this has not been proved.
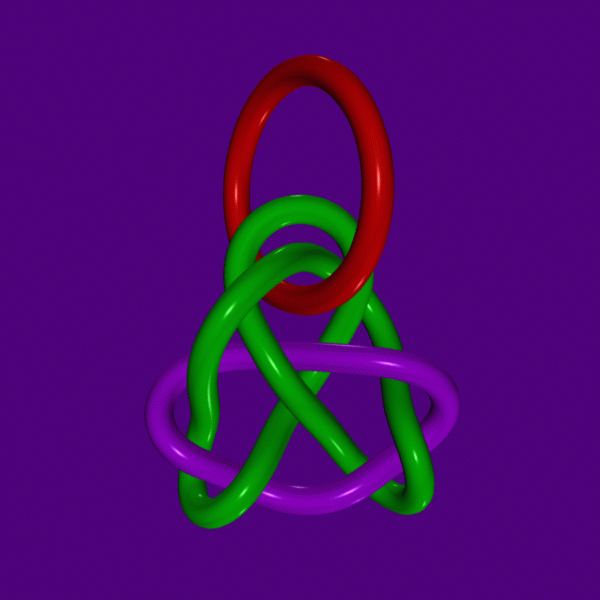
A 15-crossing non-alternating link whose canonical cell decomposition
also consists of a single ideal cube-octahedron. Here the symmetry group
of both link and manifold is the Klein group (of order 4.)